"INTRODUCCIÓN"

El término “gráfico” tiene varios sentidos en matemáticas. Hemos usado el término “gráfica” en el sentido de una relación o de una función. En este trabajo introducimos la palabra “grafo” con un sentido muy especial el cual comentaremos más adelante.

En muchas partes de la ciencia de los computadores y de la informática aparecen los grafos, especialmente los grafos de árbol, y los grafos dirigidos.

Desafortunadamente no existe una terminología estandarizada en la teoría de los grafos, por lo tanto es oportuno aclarar que las presentes definiciones pueden variar ligeramente entre diferentes publicaciones de estructura de datos y de teoría de grafos, pero en general se puede decir que un grafo como indica su nombre lo indica es la representación (para nuestro caso) gráfica de los datos de una situación particular.

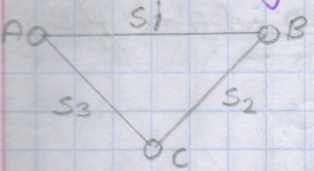
 Por ejemplo:

Los datos contienen, en algunos casos, relaciones entre ellos que no son necesariamente jerárquicos. Por ejemplo, supongamos que unas líneas aéreas realizan vuelos entre las ciudades conectadas por líneas la estructura de datos que refleja está relación recibe el nombre de grafo.

En este trabajo se tratará de explicar lo que son los grafos, sus tipos, y algunas derivaciones de ellos, así como su representación gráfica.

*********GRAFOS********

¿Qué es un grafo?

Un grafo es una estructura de datos que almacena datos de dos tipos:

     Vértices o puntos, con un valor almacenado.

     Aristas o arcos: cada una conecta a un vértice con otro, y puede tener un valor almacenado.

·        Una arista es un par de vértices (v,w)

·        Si el par está ordenado, se dice que el grafo es dirigido o que es un dígrafo.

Los grafos tienen gran cantidad de aplicaciones por ejemplo:

·        Representación de circuitos electrónicos analógicos y digitales.

·        Representación de caminos o rutas de transporte entre localidades.

·        Representacion de redes de computadoras

¿De que consta?

Un grafo consta de dos cosas:

a)     Un conjunto N cuyos elementos se llaman nodos, vértices o puntos.

b)    Un conjunto S de parejas no ordenadas de nodos diferentes, llamadas segmentos o aristas.

ü Denotamos un grafo por G(N, S) cuando queremos destacar las dos partes de G.

ü Representamos de una manera natural los grafos por diagramas en el plano. O sea, cada nodo v de N se representa por un punto (o pequeño círculo) y en cada segmento s={v_1, v₂} se representa por una curva que conecta sus terminales v_{1 y} v_2.

Los nodos A y B son adyacentes si hay un segmento {a,b}

·        Segmento es la curva que une dos nodos.

********LAZO O BUCLE********

Un lazo o un bucle en un grafo es un enlace cuyos puntos finales son el mismo nodo.

Un grafo se dice simple si no tiene lazos y existe como mucho un enlace entre cada par de nodos (no hay enlaces en paralelo)

Es una arista o arco cuyos extremos son el mismo vértice.

********CAMINO*********

Un camino es una sucesión de vértices tal que cada uno de sus vértices existe una arista hacia el vértice sucesor.

Dos caminos son independientes si no tienen ningún vértice en común excepto el primero y el último.

Un camino en un multígrafo consta de una sucesión alternada de nodos  y segmentos de la forma

                        v_0, e_1,v₁,e_2,v_{2…………………………………………………}e_n-1,v_n-1,e_n,V_n 

En donde cada segmento s_i es incidente en v_i-1 y v_i. El número n de segmentos se llama la longitud del camino. Cuando no hay ambigüedad denotamos un camino por una sucesión de segmentos (s_1,s_2, ……s_n) o por sucesión de nodos (v_1,v_2,….. v_n)_. 

Un camino P={v₀,v₁,v₂,….v_n) es simple si todos los nodos que forman el camino son distintos pudiendo ser iguales v₀ y v_n (los extremos del camino).

La longitud de un camino es el número de enlaces que tiene el camino. Por ejemplo (1, 2, 5, 1, 2, 3) es un camino con longitud 5, y (5, 2, 1) es un camino simple de longitud 2.

*CAMINO CERRADO*

El camino  se dice que es cerrado si v₀=v_n. De otro modo, decimos que el camino va de v₀ a v_n, o entre v₀ y v_n o que conecta a v₀ con v_n.

*******CAMINO SIMPLE********

Es un camino en el que todos los nodos contenidos son diferentes, con la posible excepción del primero y del último, que podrían ser el mismo.

*********CICLO*****

Un ciclo  (o circuito) es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 son los lazos (o bucles). En el ejemplo, C1 = (1,2,3,4,5,2,1) es un ciclo de longitud 6.

Un ciclo simple es un ciclo que tiene como longitud al menos 3 y en el que el nodo del comienzo solo aparece una vez más y como nodo final, y los demás solo aparecen una vez. En el grafo C2 = (1,5,2,1) es un ciclo simple.

Un grafo se dice acíclico si no contiene ningún ciclo simple.

**********GRAFO CONEXO*******

Un grafo G es conexo si y solo si sus nodos n_i no pueden ser divididos en dos conjuntos no vacíos N1 Y N2 en los que sus caminos desde un punto cualquiera.

Un grafo es conexo si cada par de vértices está conectado por un camino; es decir, si para cualquier par de vértices (a, b), existe al menos un camino posible desde a hacia b.

Un grafo es doblemente conexo si cada par de vértices está conectado por al menos dos caminos disjuntos; es decir, es conexo y no existe un vértice tal que al sacarlo el grafo resultante sea disconexo.

Es posible determinar si un grafo es conexo usando un algoritmo Búsqueda en anchura (BFS) o Búsqueda en profundidad (DFS).

En términos matemáticos la propiedad de un grafo de ser (fuertemente) conexo permite establecer con base en él una relación de equivalencia para sus vértices, la cual lleva a una partición de éstos en "componentes (fuertemente) conexas", es decir, porciones del grafo, que son (fuertemente) conexas cuando se consideran como grafos aislados. Esta propiedad es importante para muchas demostraciones en teoría de grafos.

*******ARBOL*******

El árbol es una estructura de datos muy importante en informática y en ciencias de la computación. Los árboles son estructuras no lineales, al contrario que los arrays y las listas enlazadas, que constituyen  estructuras lineales.

Los árboles se utilizan para representar fórmulas algebraicas, para organizar objetos en orden de tal forma que las búsquedas sean muy eficientes y en aplicaciones diversas tales como inteligencia artificial o algoritmos de cifrado. Casi todos los sistemas operativos almacenan sus archivos en árboles o estructuras similares a árboles. Además de las aplicaciones citadas, los árboles se utilizan en diseño de compiladores, procesado de texto y algoritmos de búsqueda.

Un árbol consta de un conjunto finito de elementos, denominados nodos y de un conjunto finito de líneas dirigidas, denominadas ramas que conectan los nodos. El número de ramas asociado con un nodo es el grado del nodo.

Si un árbol no está vacío entonces se le llama raíz. Un árbol puede representar diversas generaciones en la familia. Los hijos de un nodo y los hijos de estos hijos se llaman descendientes y el padre y los abuelos de un nodo son sus ascendientes.

*****************Nomenclatura sobre árboles********************

                                         

- Raíz: es aquel elemento que no tiene antecesor; ejemplo: a. 
- Rama: arista entre dos nodos. 
- Antecesor: un nodo X es antecesor de un nodo Y si por alguna de las ramas de X se puede llegar a Y.
- Sucesor: un nodo X es sucesor de un nodo Y si por alguna de las ramas de Y se puede llegar a X.
- Grado de un nodo: el número de descendientes directos que tiene. Ejemplo: c tiene grado 2, d tiene grado 0, a tiene grado 2.
- Hoja: nodo que no tiene descendientes: grado 0. Ejemplo: d
- Nodo interno: aquel que tiene al menos un descendiente.
- Nivel: número de ramas que hay que recorrer para llegar de la raíz a un nodo. Ejemplo: el nivel del nodo a es 1 (es un convenio), el nivel del nodo e es 3.
- Altura: el nivel más alto del árbol. En el ejemplo de la figura 1 la altura es 3.
- Anchura: es el mayor valor del número de nodos que hay en un nivel

*************Árboles Binarios*****************

Los árboles ordenados de grado dos son conocidos como árboles binarios. En un árbol binario cada nodo puede tener como máximo dos subárboles y estos se distinguen entre sí como el subárbol izquierdo y el subárbol derecho, según su ubicación con respecto al nodo raíz.

Los árboles binarios tienen múltiples aplicaciones. Por ejemplo: para representar la solución de un problema, en el cual existen dos posibles alternativas; para representar un árbol genealógico, un árbol binario de búsqueda y un árbol binario que represente expresiones.

*Árboles binarios distintos, similares y equivalentes*

Arboles binarios distintos.-cuando en sus estructuras la distribución de nodos y arcos son diferentes.

Árboles binarios similares.-cuando sus estructuras son idénticas, pero la información que contienen sus nodos difiere entre sí.

Arboles binarios equivalentes.-son aquellos que son similares y además los nodos contienen la misma información.

**********GRAFO COMPLETO**********

Un grafo es completo si cada nodo está conectado con todo otro nodo. Al grafo completo de n nodos se le denota K_n. La figura muestra los grafos K_1, K_2,......K_6. Al grafo K_1, un nodo aislado, se le llama el grafo trivial.

El conjunto de los grafos completos es denominado usualmente , siendo   el grafo completo de n vértices.

Un   , es decir, grafo completo de n vértices tiene exactamente   aristas.

La representación gráfica de los   como los vértices de un polígono regular da cuenta de su peculiar estructura.